オンラインで受けることができる最も信憑性があるであろうMENSA公式のテストがノルウェーメンサのIQテストです。
JAPAN MENSAの過去問は公開されていないため、自分がMENSAに受かる可能性があるか腕試しをしてみたい方はノルウェーメンサの問題に挑戦してみると良いと思います!
この記事では現役メンサ会員のブログ主がノルウェーメンサのオンラインテストの解き方を日本語で解説していきます!
(既に他のサイトで解説している方がいますが論理的破綻が多くみられるので私が作った解説を参照するのが間違いないと思います)
コメント欄では別解なども受け付けていますので、そちらも是非参考にしてみてください。
問題を解くときに必ず意識すること
1.上段・中段・下段に分割して考える。
2.上段、中段から行方向の法則性を見つけ、その法則を下段にも適用する。
3. 列方向のグルーピングも行い、列方向の法則も発見して全体として整合性がとれていることを確認する(列方向または行方向のみでしかグルーピングできない問題も稀にあるので注意)。
+α.他に別解がないか問題研究を行ってみよう。
解説は簡潔にまとめています。理解できない問題があったときはしばらく頭の中に残して、インターネットで類似した問題を検索したり、他に考えうる解法はないかと図解してみたり、自分の手と頭を使って得たものが真に自身の力となり、それ故じっくり考え抜くことがIQ向上のための最大の学習になると私は考えています。わからなかった問題は解説をじっくり見ながらウンウン頭を捻って考えましょう!
Exercise 1
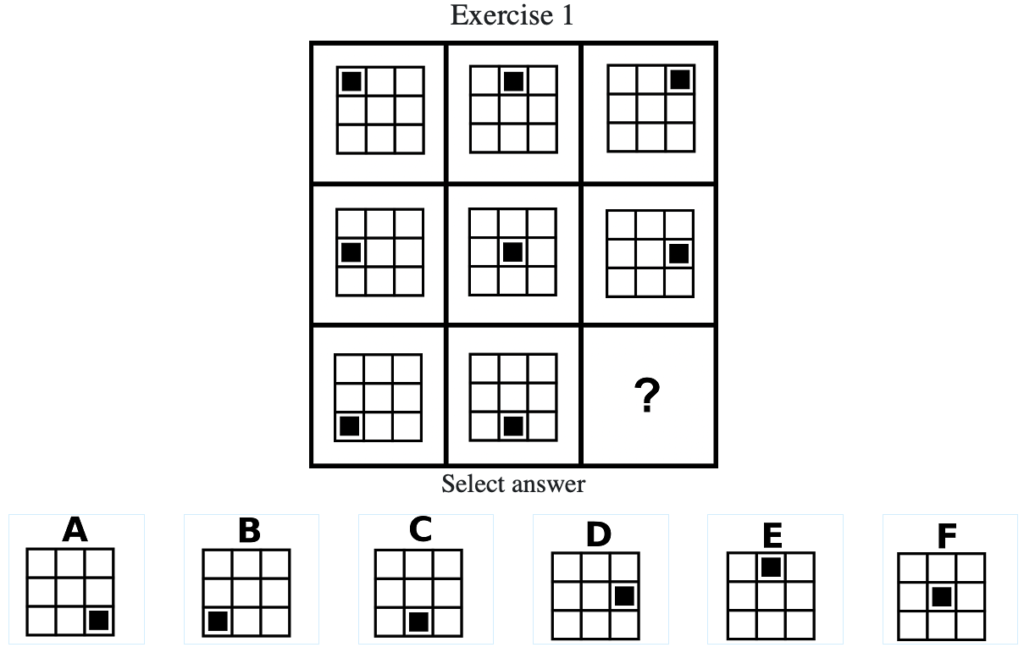
答え:「A」
解説:上中段と同様の法則で下段も黒マスが1マスずつ右へ移動しているため答えは「A」となる。(列方向でグルーピングした場合は黒マスが1マスずつ下に移動しているので整合性が取れている。)
Exercise 2
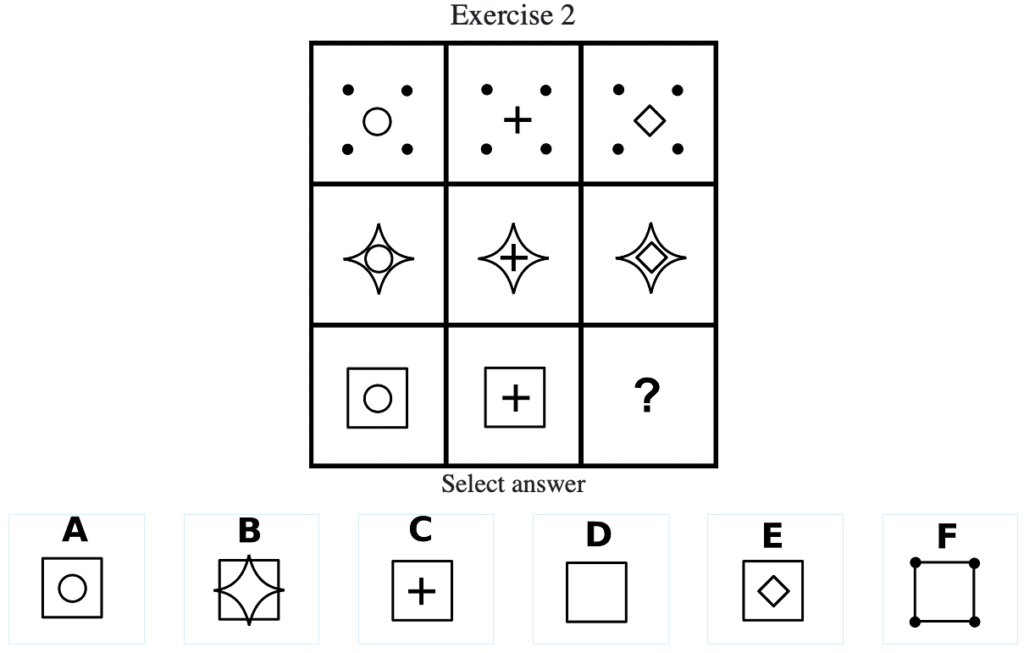
答え:「E」
解説:上中段から、行ごとに外枠が共通しており、中心の記号が「丸」→「十字」→「菱形」→「丸」→…の順に変化する法則があることがわかる。したがって外枠は四角で中心は菱形であると推察できるので「E」となる(列方向にグルーピングした場合は中心の記号はそのままに外枠が変化する法則がある)。
Exercise 3
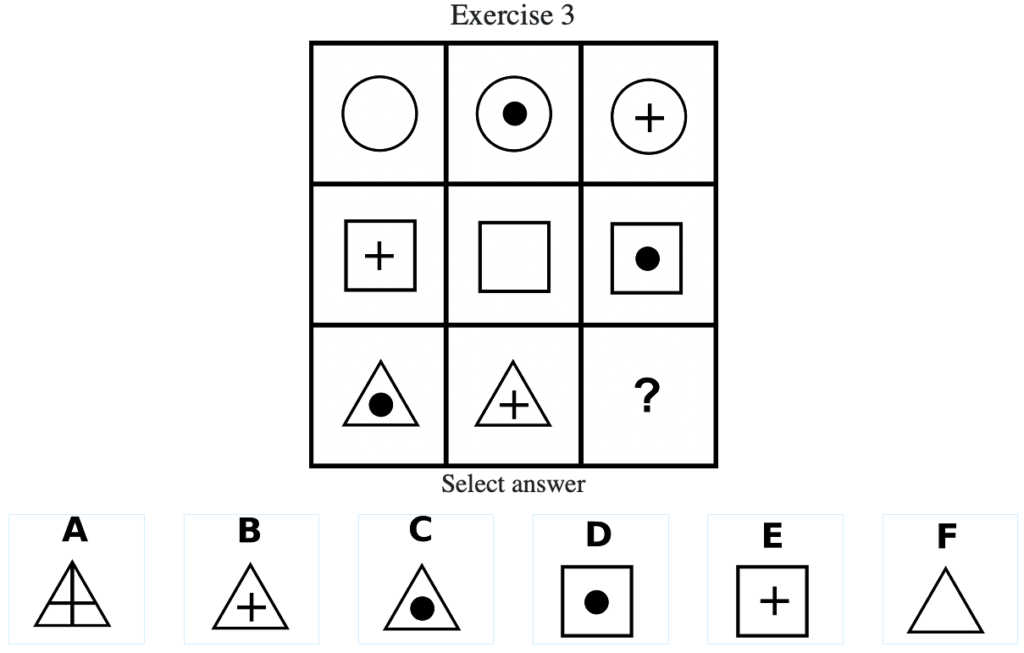
答え:「F」
上中段から、行ごとに外枠が同じであり、中心の記号が「なし」→「丸」→「十字」→「なし」→…の順にループする法則があることがわかる。したがって答えは外枠は三角で中心は「なし」であると推察できるので「F」となる(列方向にグルーピングした場合は外枠が「丸」→「四角」→「三角」→「丸」→…の順にループし、中心の記号は「なし」→「十字」→「丸」→「なし」→…の順にループする法則がある)。
Exercise 4
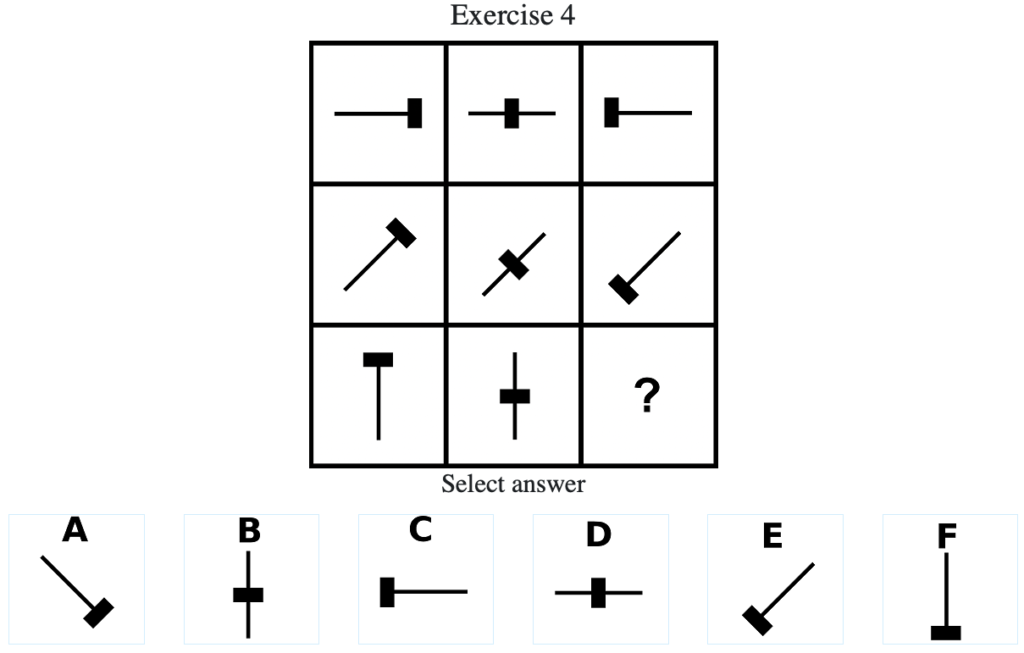
答え:「F」
解説:上中段から、黒色の長方形が棒線上を「右」→「真ん中」→「左」→「右」→…の順に移動する法則があることがわかる。したがって下段では「上」→「真ん中」→「下」→「上」→…の順に移動することが推測されるので答えは「F」となる(列方向にグルーピングした場合は棒線が班時計回りに45度ずつ動く法則がある)。
Exercise 5
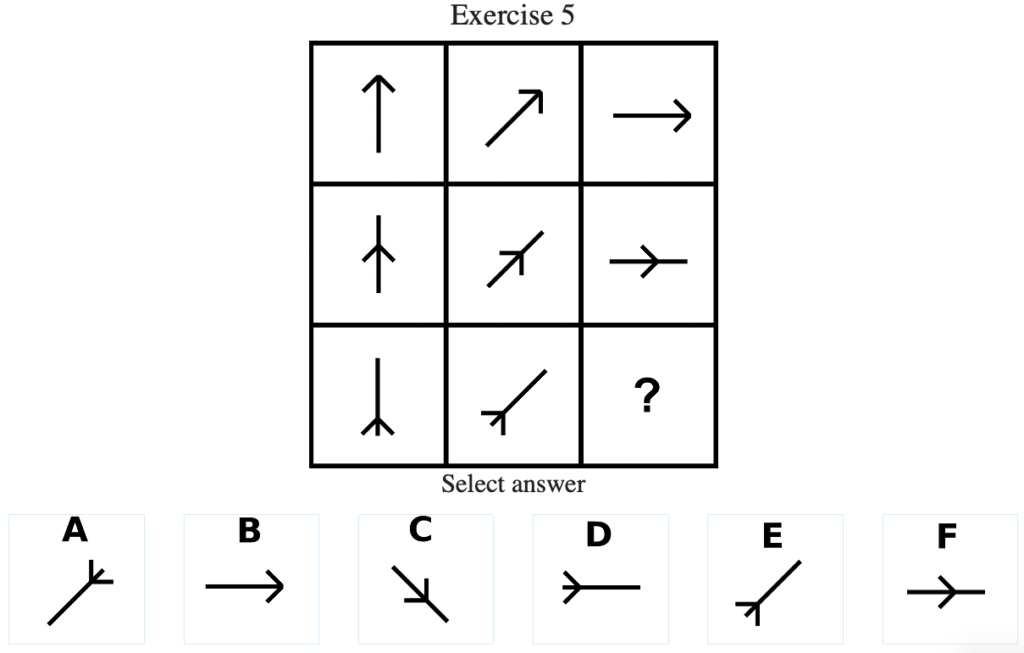
答え:「D」
解説:上中段より、時計回りに45度ずつ回転するので答えは「D」となる(列方向にグルーピングした場合は「^」が下に落ちてくる法則がある。)
Exercise 6
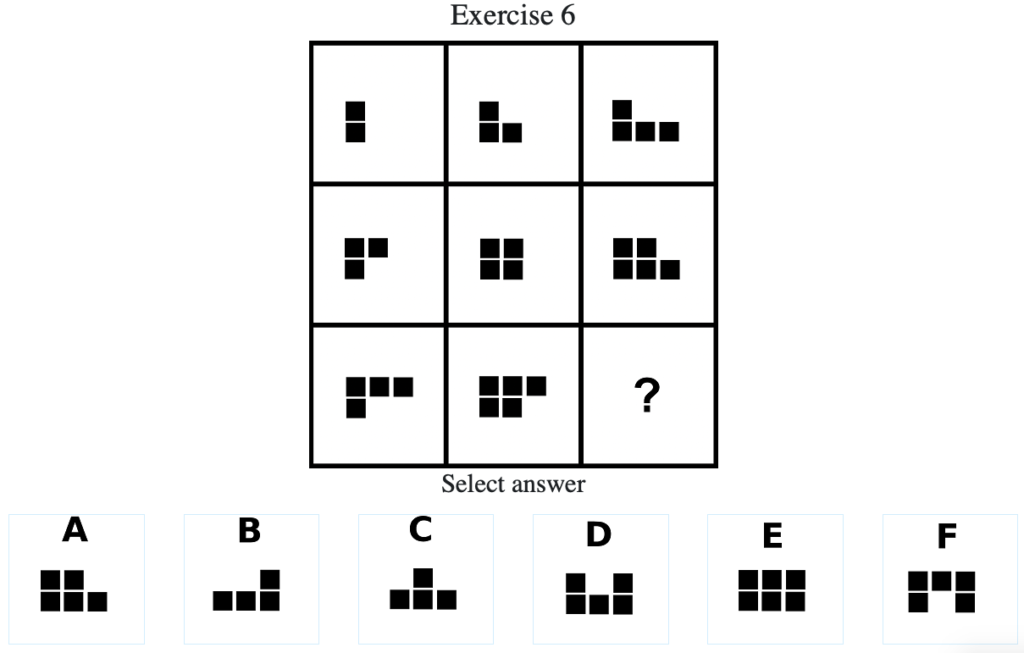
答え:「E」
解説:上中段から、順に黒色のマスが1つずつ増えることがわかるので答えは「E」となる(列方向にグルーピングした場合も同様である)。
Exercise 7
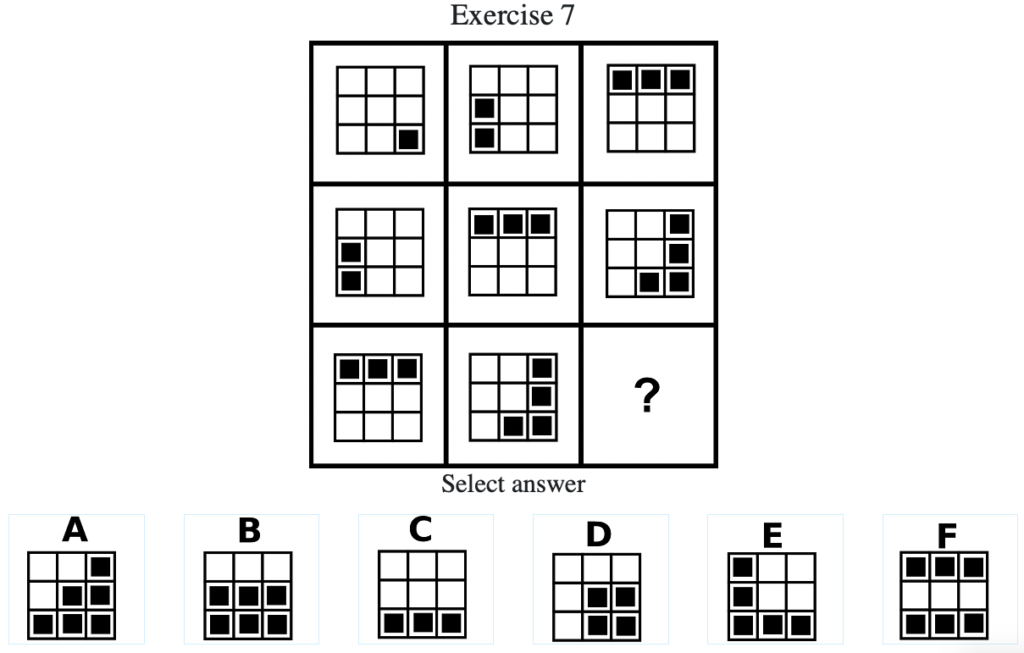
答え:「E」
解説:上中段から、黒マスが一つずつ増えて黒マスの開始地点が時計回りに90度回転することがわかる。したがって答えは「E」となる(列方向にグルーピングした場合も同様であるため整合性が取れる)。
Exercise 8
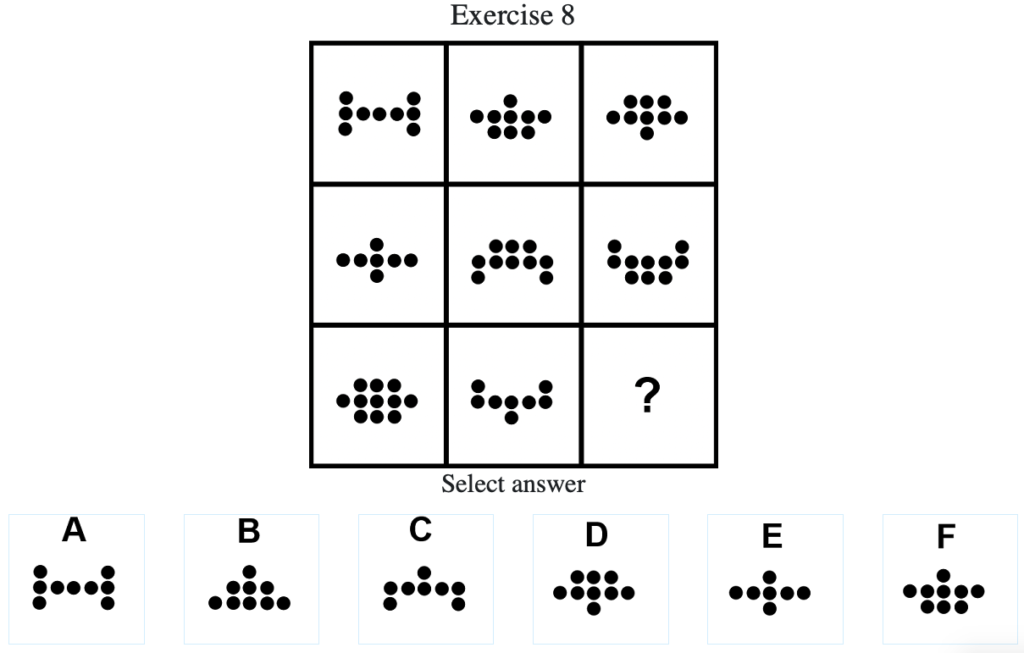
答え:「C」
各マス内の上部の点と下部の点の個数のパターンの変化に注目する。上中段よりマス内の上部の点は「・ ・」→「 ・ 」→「 ・・・ 」→「・ ・」→…の順に変化し、マス内の下部の点は「・ ・」→「 ・・・ 」→「 ・ 」→「・ ・」→…の順に変化する。したがって答えは上部の点が「 ・ 」かつ下部の点が「・ ・」の「C」となる(列方向にグルーピングした場合も同様に「・ ・」→「 ・ 」→「 ・・・ 」→「・ ・」→…の順に変化し、マス内の下部の点は「・ ・」→「 ・・・ 」→「 ・ 」→「・ ・」→…の順に変化する)。
Exercise 9
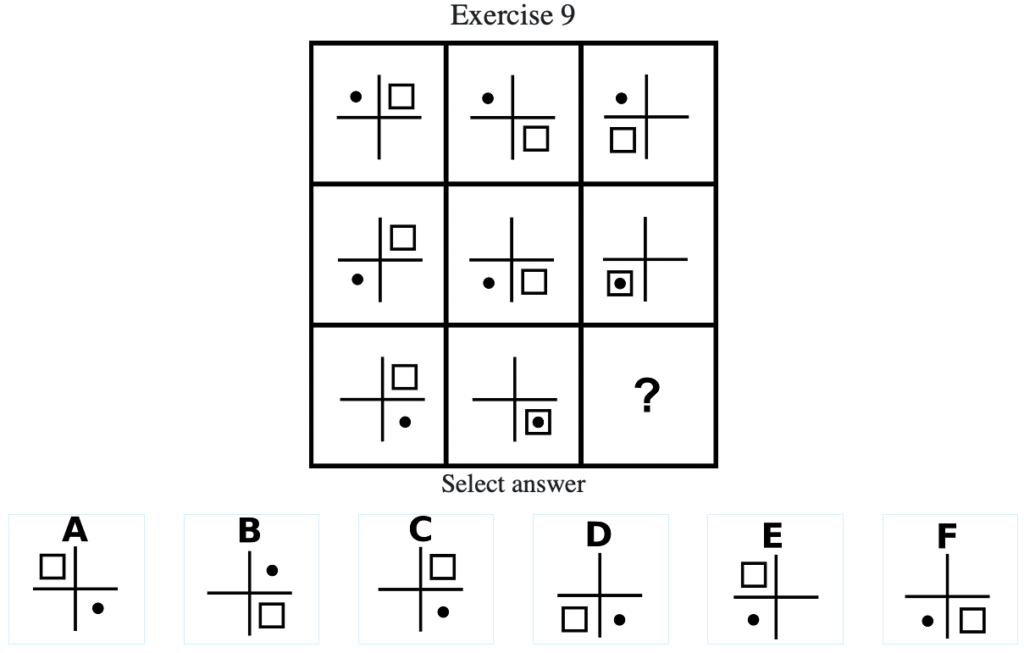
答え:「D」
解説:上中段より、黒点は固定のまま、四角形だけが時計回りに移動する。したがって黒点は右下に固定のまま四角形が左下にある「D」となる(列方向にグルーピングした場合は四角形が固定で黒点が反時計回りに移動する)。
Exercise 10
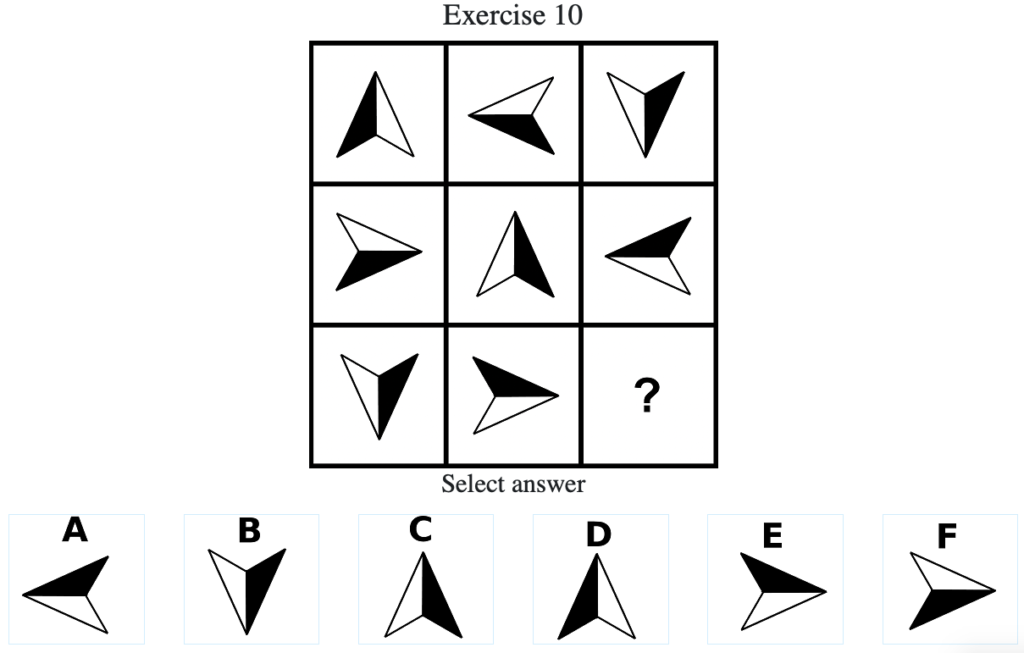
答え:「D」
解説:上中段から、矢印は反時計回りに90度ずつ回転することがわかる。したがって答えは「D」となる(列方向にグルーピングした場合は黒と白が交互に入れ替わりながら時計回り)。
Exercise 11
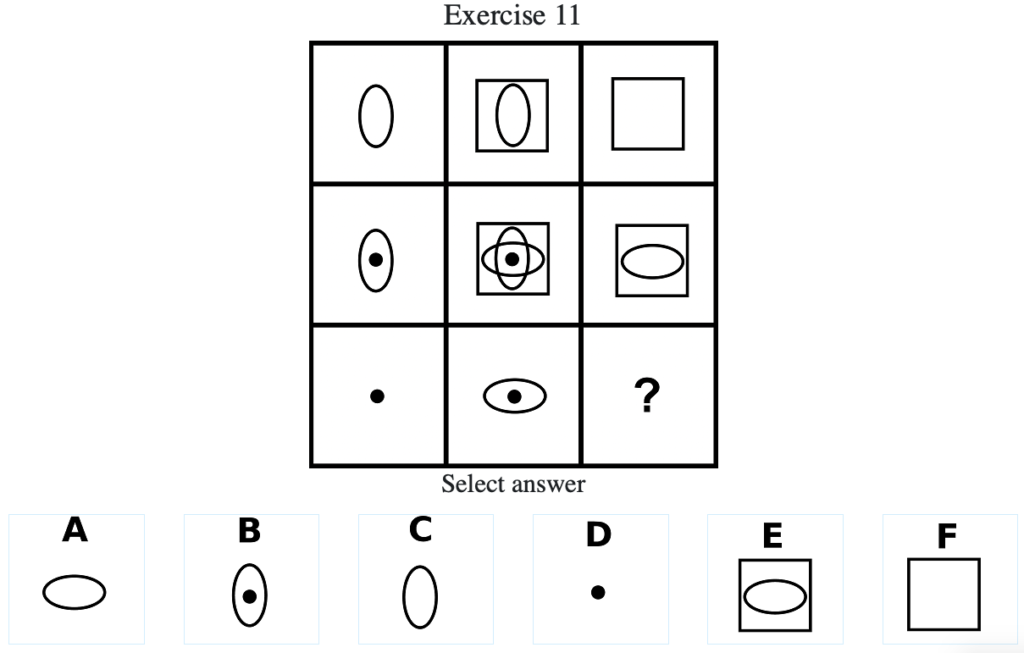
答え:「A」
解説:上中段より、左列の図形と中央列の図形を重ね合わせて重複した部分は打ち消され、右列の図形になる。したがって答えは「A」となる(列方向にグルーピングした場合も同様に上段と中段を重ね合わせて、重複した部分は打ち消されて下段の図形となる)。
Exercise 12
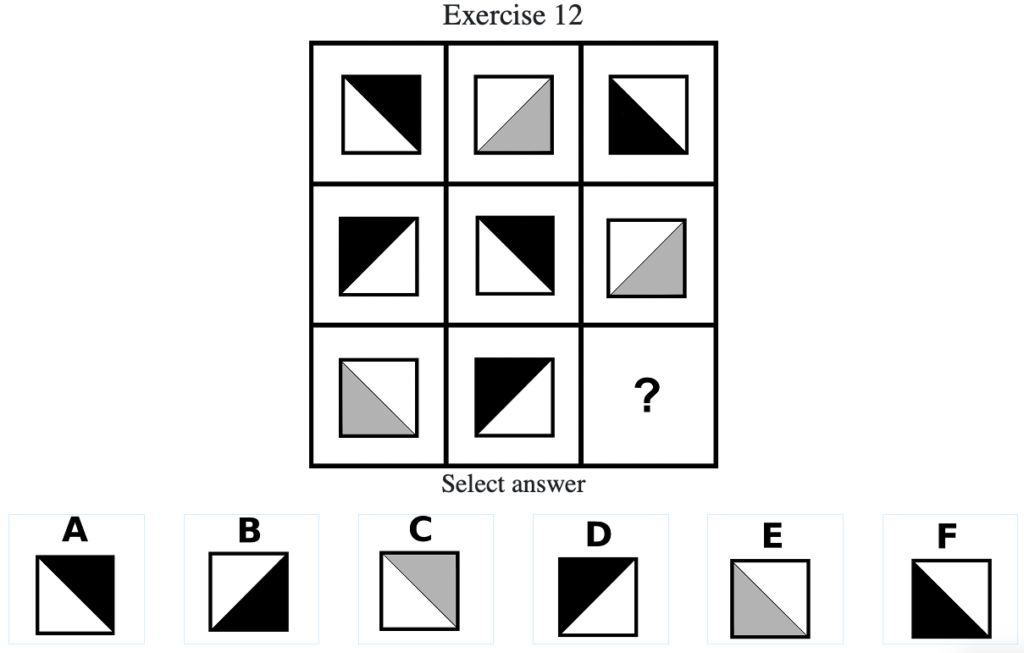
答え:「A」
解説:上中段から、図形は時計回りに90度回転し、「黒」→「灰」→「黒」→「黒」→…の順にループして色が変わることがわかる。したがって右下のマスの右端の色が「黒」になることが推測されるので答えは「A」となる(列方向にグルーピングした場合は反時計回り)。
Exercise 13
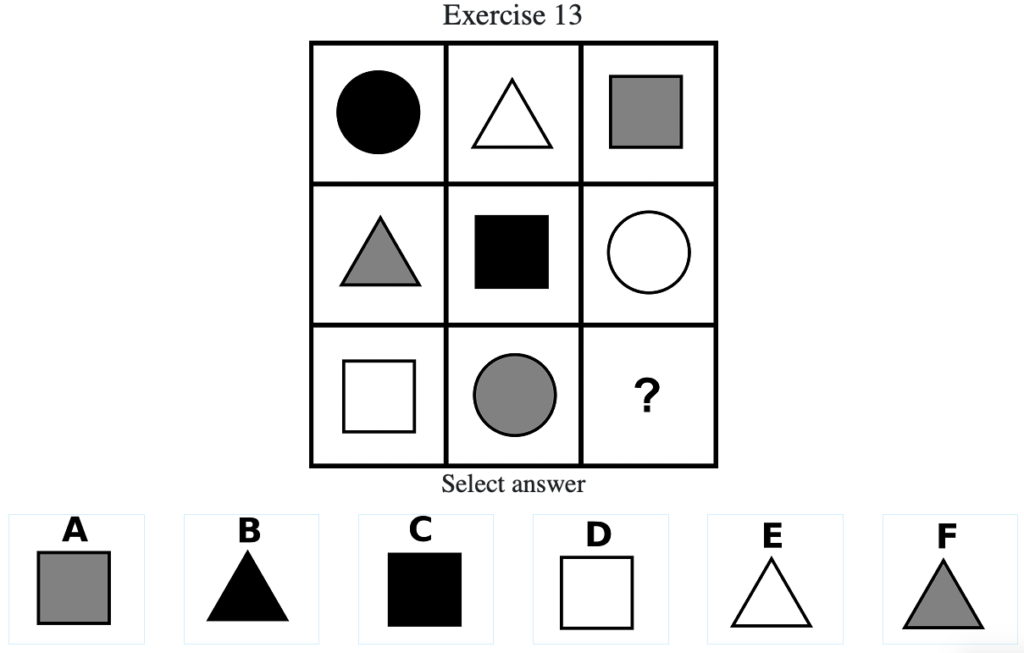
答え:「B」
解説:上中段から、図形は「丸」→「三角」→「四角」→「丸」→…の順に変化し、図形の色は「黒」→「白」→「灰」→「黒」→…の順に変化する法則があることがわかる。したがって答えは形が「三角」で色が「黒」のある「B」となる (列方向にグルーピングした場合は図形は「丸」→「三角」→「四角」→「丸」→…の順に変化し、図形の色は「黒」→「灰」→「白」→「黒」→…の順に変化する)。
Exercise 14
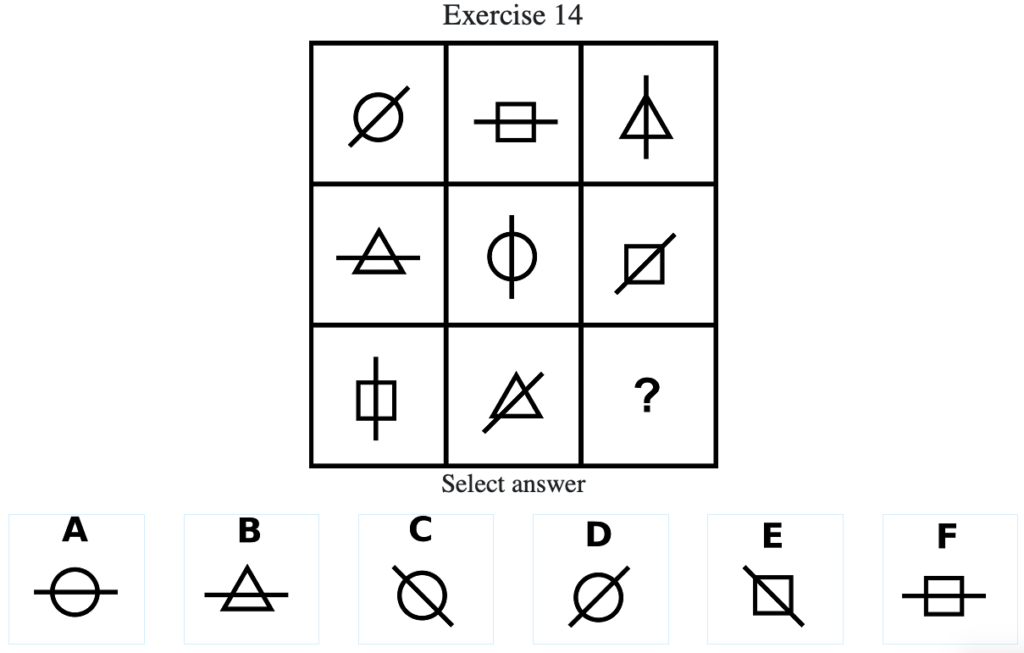
答え:「A」
解説:上中段から、棒線は「斜め」→「横」→「縦」→「斜め」→…の順に遷移し、図形は「丸」→「四角」→「三角」→「丸」→…の順に変化する法則があることがわかる。したがってその法則をもとに考えると答えは棒線が「横」で図形の形が「丸」である「A」となる(列方向にグルーピングした場合は棒線は「斜め」→「横」→「縦」→「斜め」→…の順に遷移し、図形は「丸」→「三角」→「四角」→「丸」→…の順に変化する)。
Exercise 15
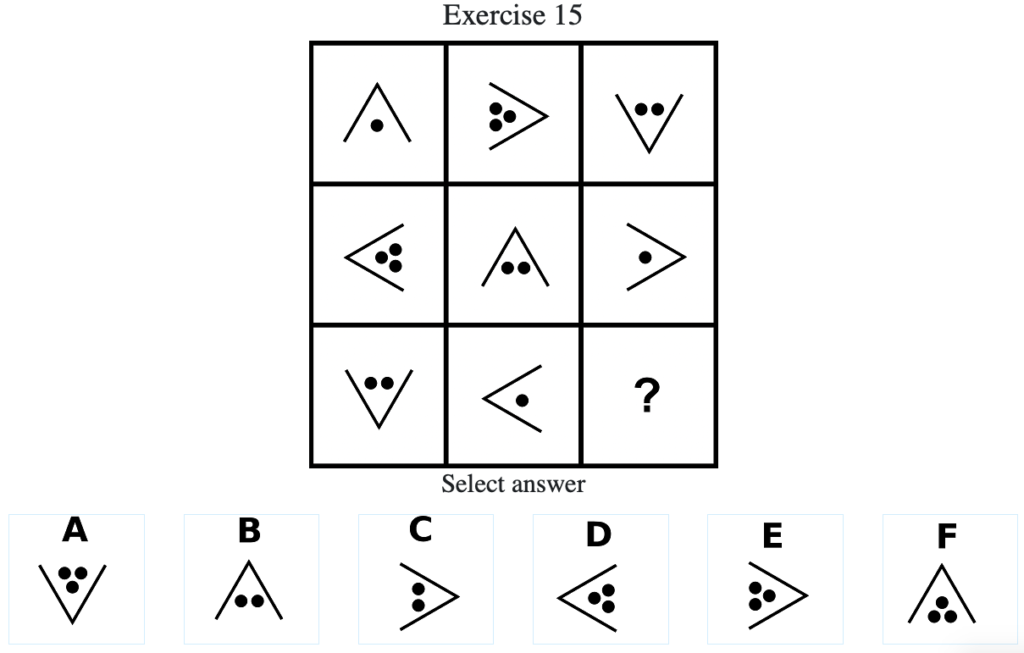
答え:「F」
解説:上中段から、外枠が時計回りに90度ずつ回転し、内側の点の個数が「1」→「3」→「2」→「1」→…の順に増減することがわかる。したがって外枠の角が上を向いており、内側の点の個数が「3」の「F」となる(列方向にグルーピングした場合は、外枠が半時計回りに90度ずつ回転し、内側の点の個数が「1」→「3」→「2」→「1」→…の順に増減する)。
Exercise 16
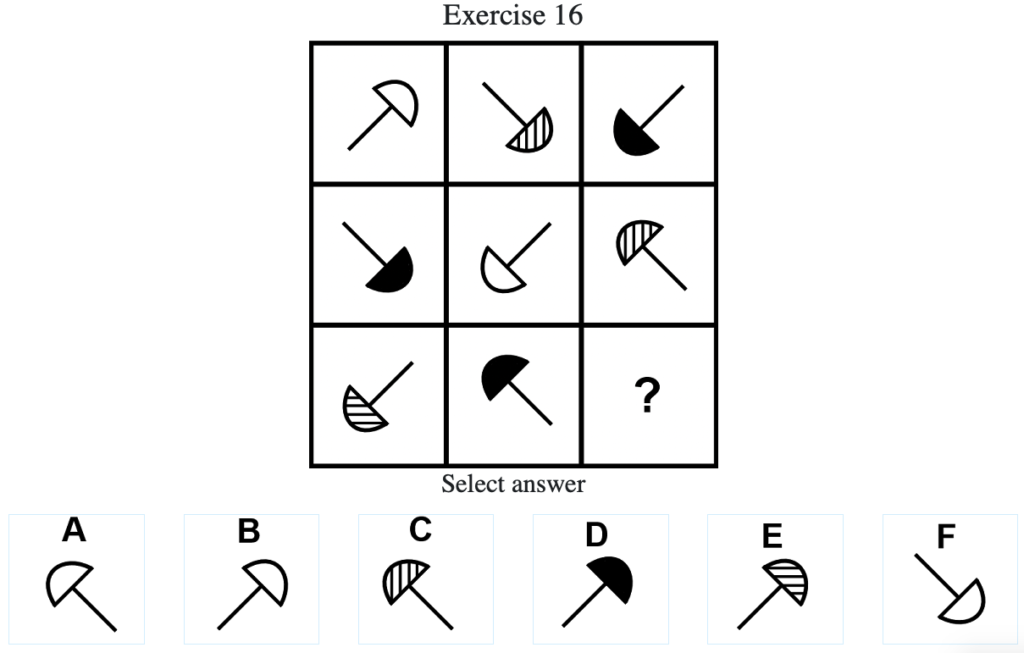
答え:「B」
解説:上中段より、棒線が時計回りに90度ずつ回転し、棒線の先にある半円の色が「白」→「斜線」→「黒」→「白」→…の順に変化する法則があることがわかる。したがって答えは半円の色が「白」で下段中央から90度時計回りに回転した「B」となる(列方向でグルーピングした場合は、棒線が時計回りに90度ずつ回転し、棒線の先にある半円の色が「白」→「黒」→「斜線」→「白」→…の順に変化する)。
Exercise 17
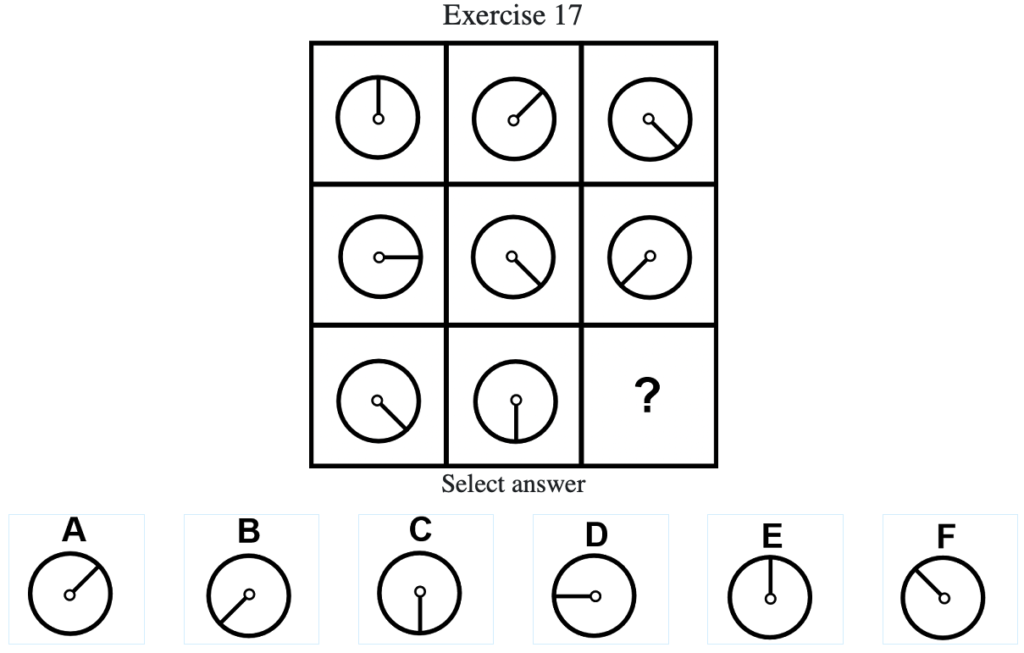
答え:「D」
解説:円の中心から伸びた棒線が時計回りに「45度」→「90度」→「45度」→…の順に回転することがわかるので答えは「D」となる(列方向でグルーピングした場合も同様に「90度」→「45度」→「90度」→「45度」→…の順に回転する)。
Exercise 18
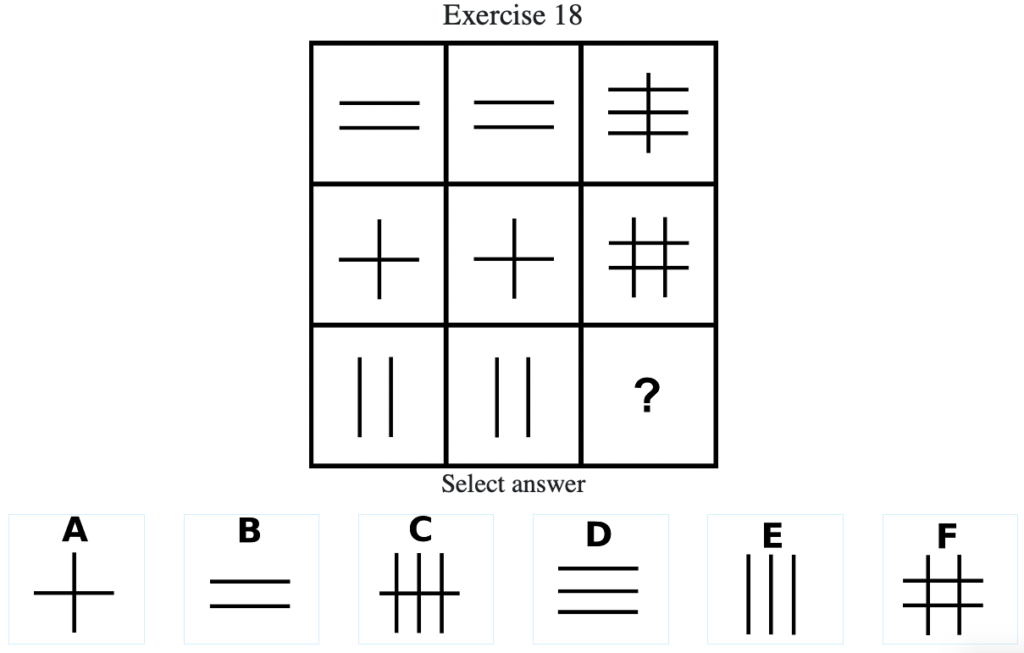
答え:「C」
解説:下段の答えは上段の画像を90度回転させた場合と同じになる。したがって答えは「C」となる(横が4本になる場合はその中の1本を縦に配置し、縦が4本になる場合はその中の1本を横に配置するという見方もできる)。
Exercise 19
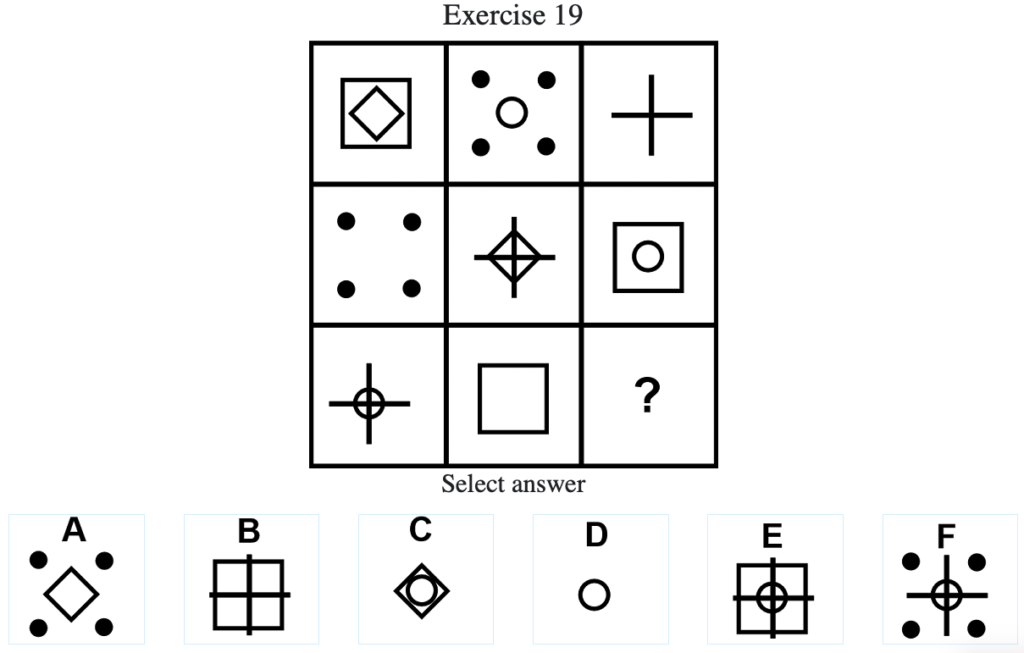
答え:「A」
解説:上中段から、外枠は「四角」→「四点」→「十字」→「四角」→…の順に変化し、中の記号は「菱形」→「丸」→「なし」→「菱形」→…の順で変化する法則が存在することがわかる。したがってこの法則を下段に適用すると外枠が「四点」で内側が「菱形」の「A」となる(列方向でグルーピングした場合は、外枠は「四角」→「四点」→「十字」→「四角」→…の順に変化し、中の記号は「菱形」→「なし」→「丸」→「菱形」→…の順で変化する)。
Exercise 20
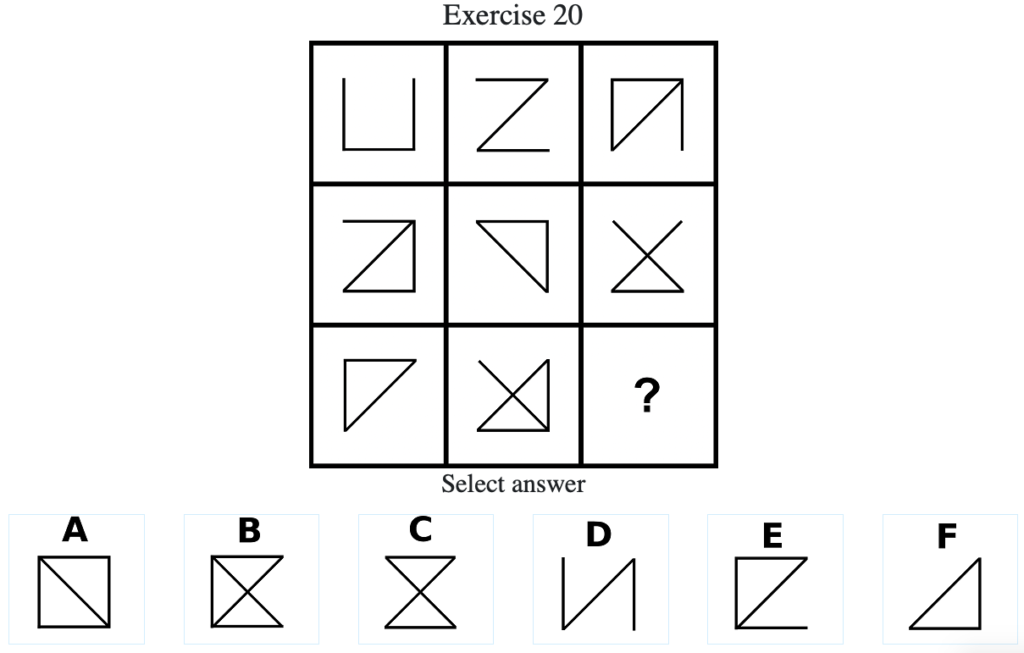
答え:「A」
解説:上中段から、左列の図形と中央の列の図形を重ね合わせて、重複した部分が打ち消されて右列の図形になるという法則があることがわかる。したがって答えは「A」となる(列方向にグルーピングした場合に関しても同様に上の行の図形と中央の行の図形を重ね合わせて、重複した部分が打ち消されて下の行の図形になる)。
Exercise 21
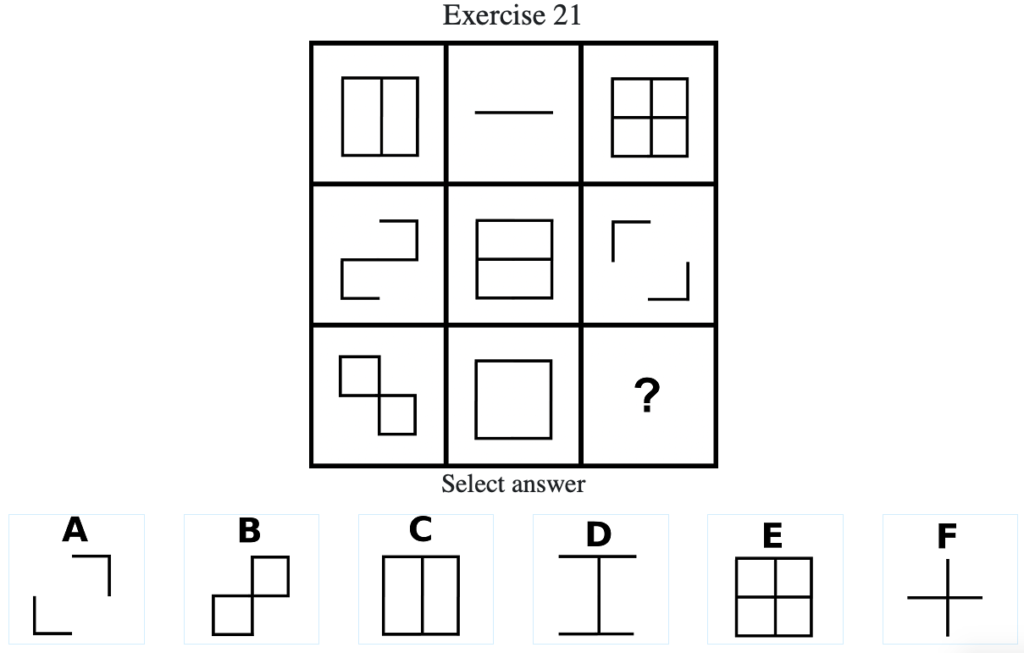
答え:「B」
解説:上中段から、左列の図形と中央の列の図形を重ね合わせて、重複した部分が打ち消されて右列の図形になるという法則があることがわかる。したがって答えは「B」となる(列方向にグルーピングした場合に関しても同様に上の行の図形と中央の行の図形を重ね合わせて、重複した部分が打ち消されて下の行の図形になる)。
Exercise 22
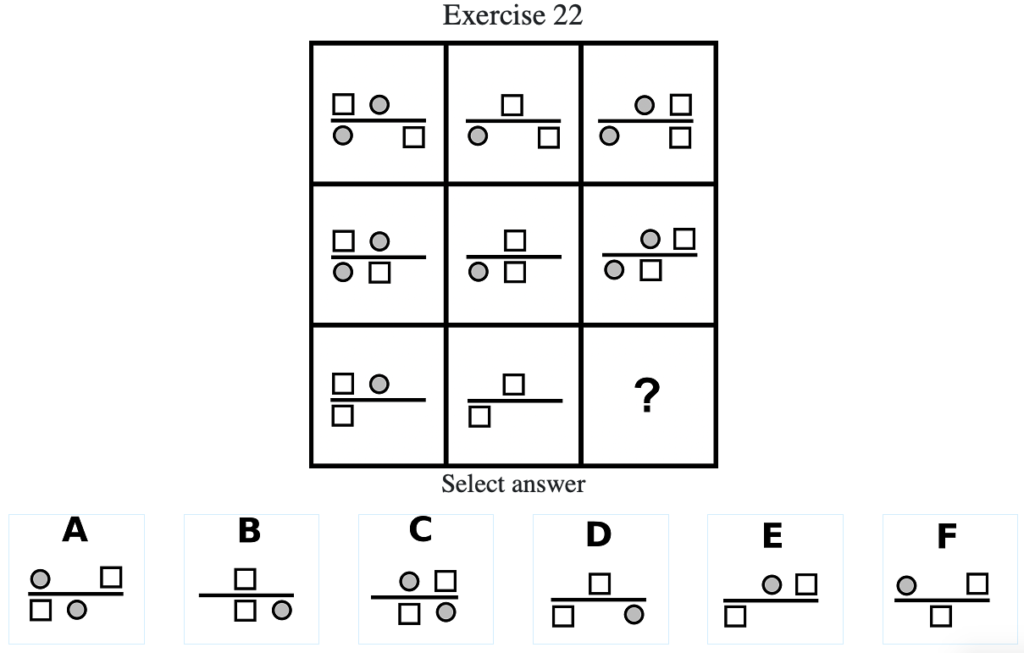
答え:「E」
解説:上中段から、マスの中央の棒線の上側の四角形のみが右に移動し、四角と丸が重なった場合は、丸は四角の下に隠れることがわかる。したがって答えは上側の四角が右の位置にある「E」となる(列方向にグルーピングした場合は棒線右下の四角形のみが左に移動する)。
Exercise 23
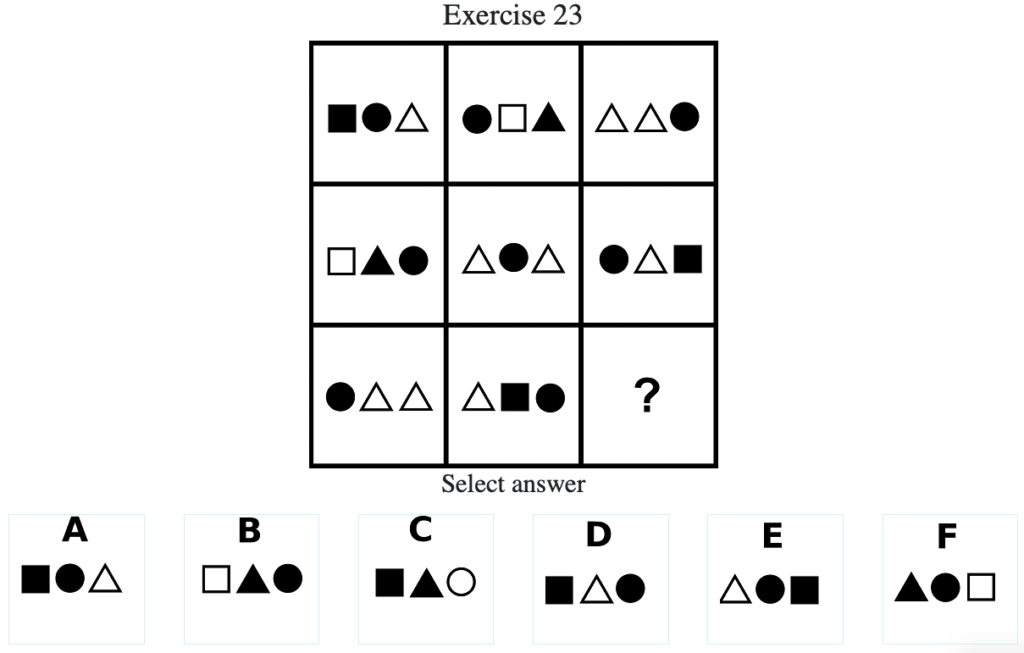
答え:「F」
解説:各マス内の3つの図形の組み合わせは「■●△」「●□▲」「●△△」の3種類であり、右上がり斜めのマスでグルーピングをすることができる。各図形は一段下がるごとに、中身の記号が1つずつ左に移動するので求める答えは「F」となる。
Exercise 24
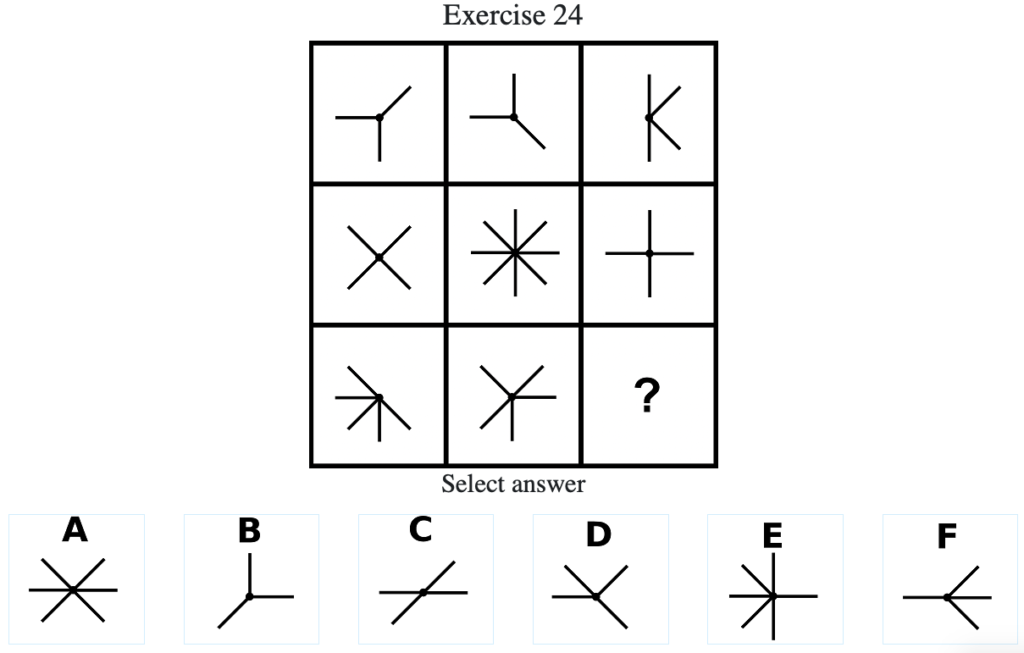
答え:「F」
解説:上中段から、左列の図形と中央列の図形を重ね合わせて、重複した部分が打ち消されて右の列の図形になる。したがって答えは下段左と下段中央を重ね合わせて、重複したところが打ち消されて「F」となる(列方向でグルーピングした場合も同様に上の行と中央の行の重複したところが打ち消されて下の行の図形になる)。
Exercise 25
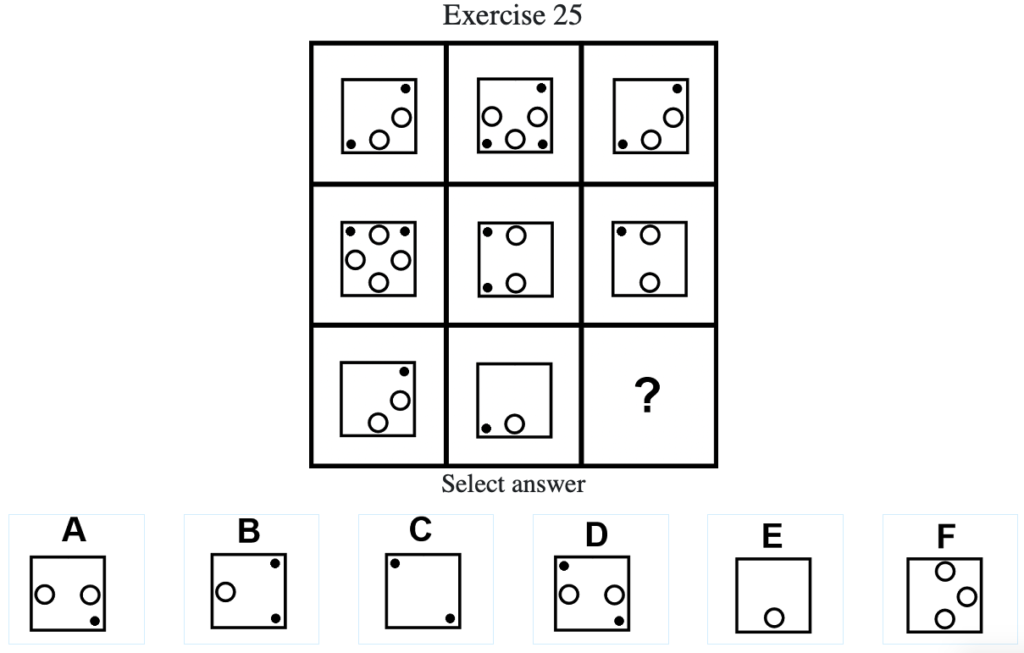
答え:「E」
解説:上中段より、左列の図形と中央列の図形を重ね合わせて、重複しなかった「・」と「◯」を消すと右列の図形になる法則がわかる。したがって答えは「E」となる(列方向にグルーピングした場合も同様に、上の行と中央の行の重複しなかった「・」と「◯」を消すことで下の行の図形になる)。
Exercise 26
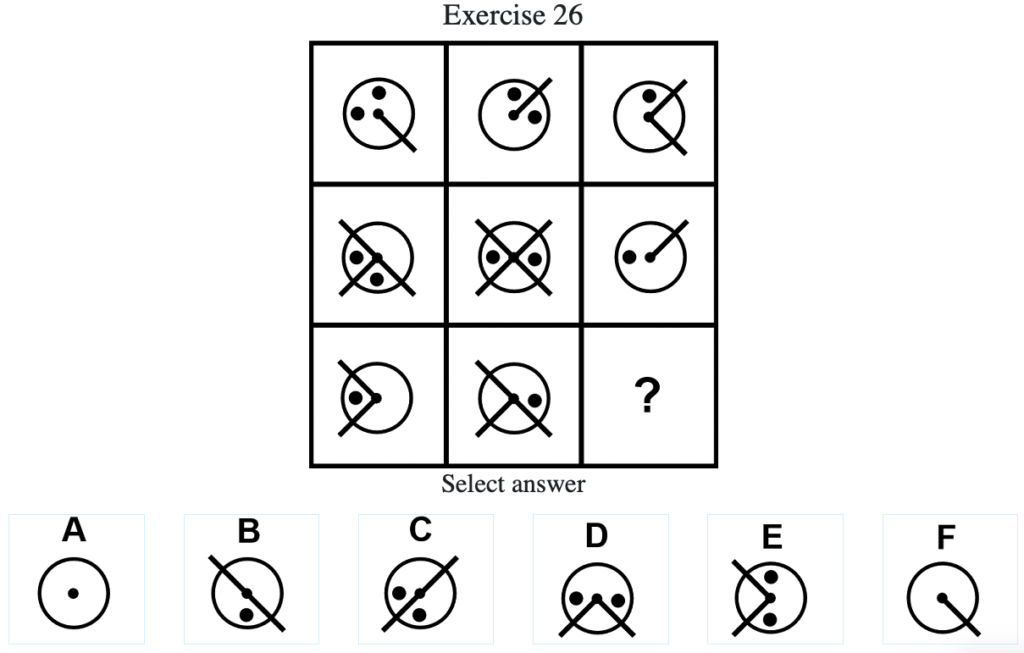
答え:「F」
解説:上中段より、左列の図形と中央列の図形を重ね合わせて、重複しなかった「・」と重複した棒線を消すと右列の図形になる法則がわかる。したがって答えは「F」となる(列方向でグルーピングした場合も同様に上の行の図形と中央の行の図形を重ね合わせて、重複しなかった「・」と重複した棒線を消すと下の行の図形になる)。
Exercise 27
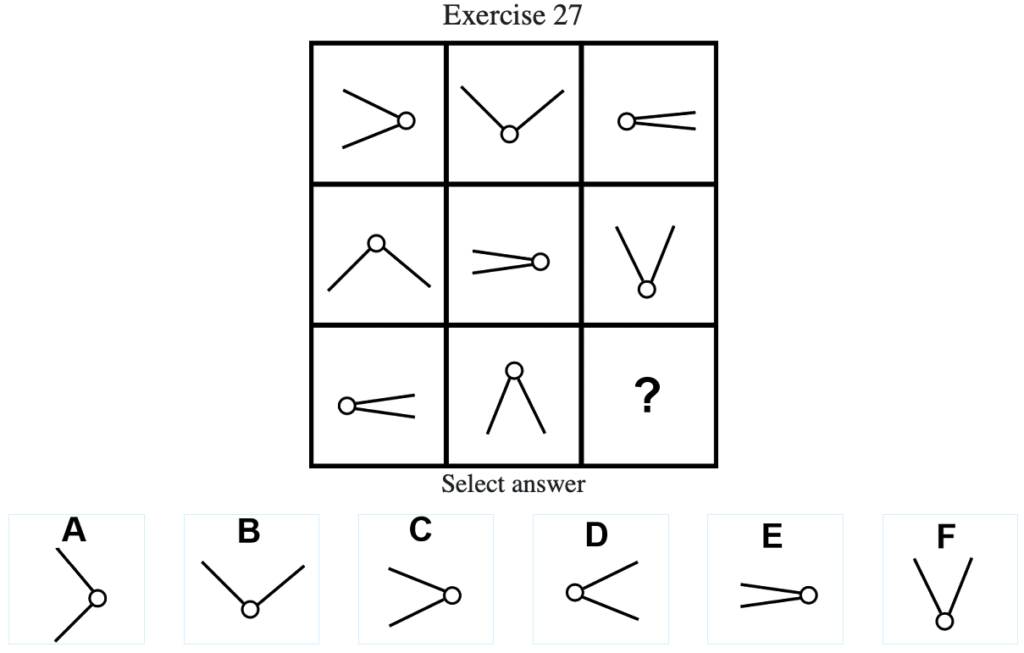
答え:「A」
解説:上中段より、記号が時計回りに90度ずつ回転し、棒線の足の開きが「小」→「中」→「大」→「小」→…の順に変化する法則がわかる。したがって答えは「A」となる(列方向でグルーピングした場合は反時計回りに90度ずつ回転する)。
Exercise 28
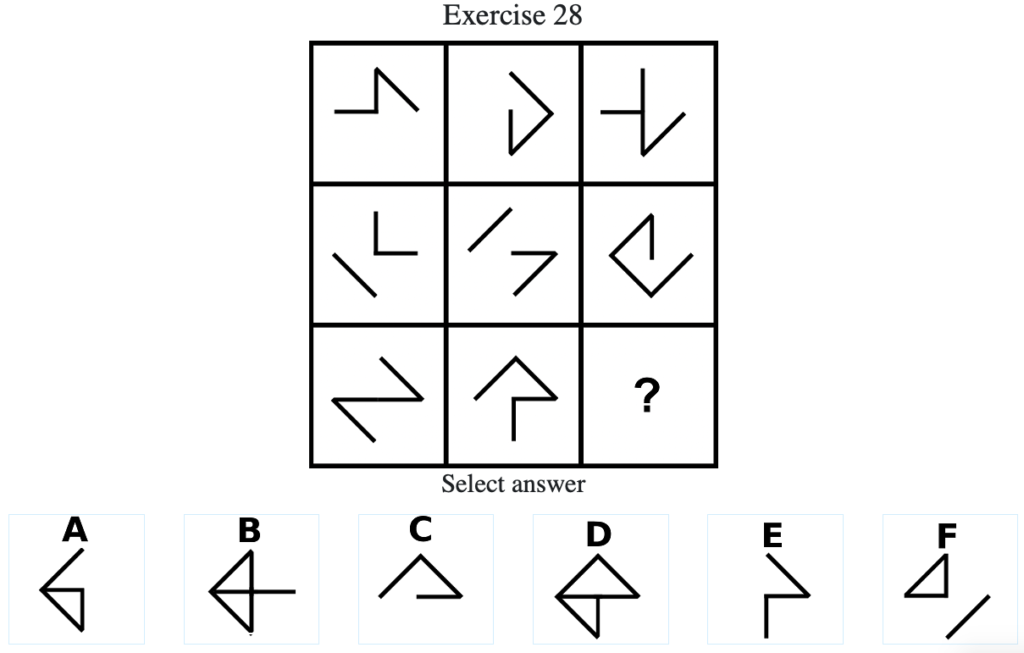
答え:「A」
解説:上中段から、左列の図形と中央列の図形を重ね合わせて、重複した部分を消すと右列の図形になる法則がわかる。したがって答えは「A」となる(列方向にグルーピングした場合も同様に上の図形と中央の図形を重ね合わせて、重複した部分を消すと下の行の図形になる)。
Exercise 29
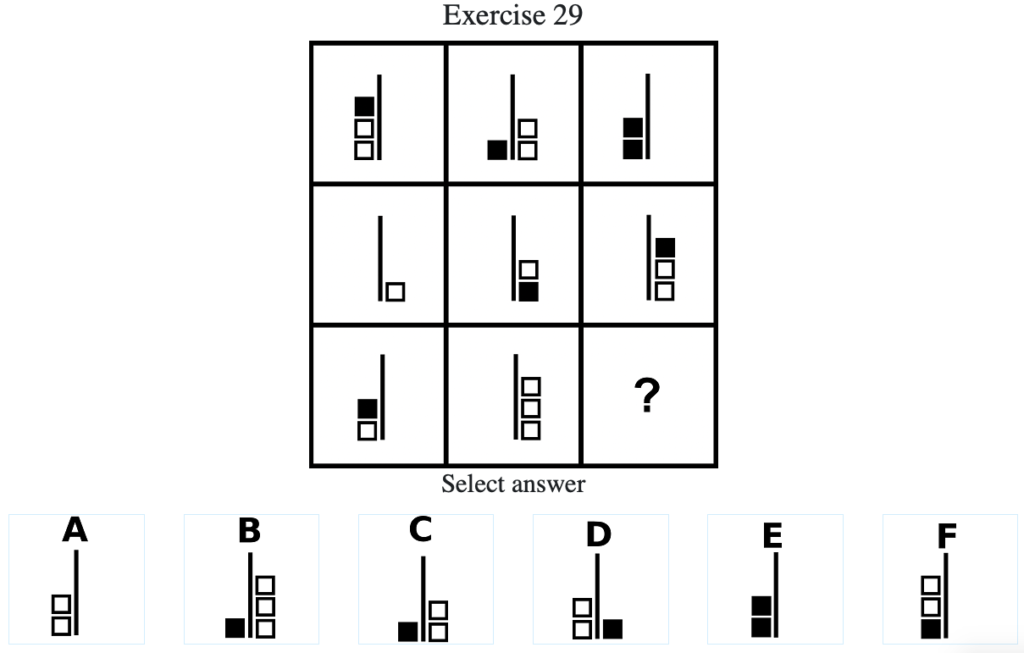
答え:「C」
解説:各マスの中央の棒線の左側の図形をプラスとしたとき、棒線の右側の図形をマイナスとして黒と白の四角の個数をそれぞれ足し合わせる(例:上段左(黒+1、白+2)+上段中央(黒+1、白-2)=上段右(黒+2、白0))と、右列の図形となる。したがって答えは「C」となる(列方向にグルーピングした場合も同様である)。
Exercise 30
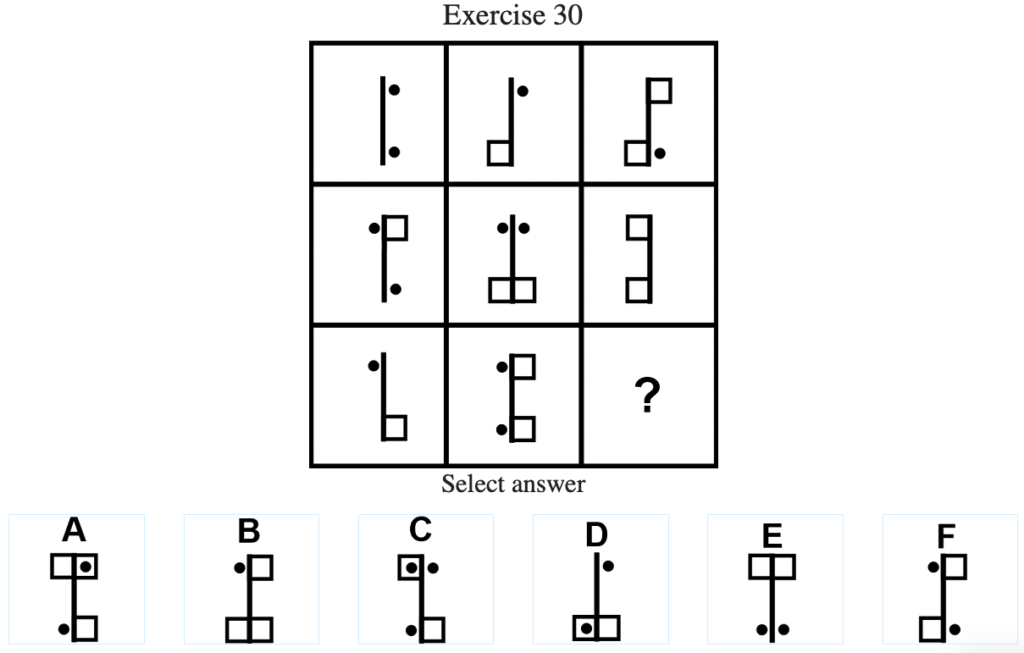
答え:「E」
解説:上中段から、左列の図形と中央列の図形を重ね合わせて、「・」と「・」が重なった場合は「□」に、「空白」と「□」が重なった場合は「□」、「□」と「・」が重なった場合は「空白」、「・」と「空白」が重なった場合は「・」に変化させると右列の図形になる法則がわかる。したがってこれを下段に適用すると答えは「E」となる(列方向にグルーピングした場合も同様である)。
Exercise 31
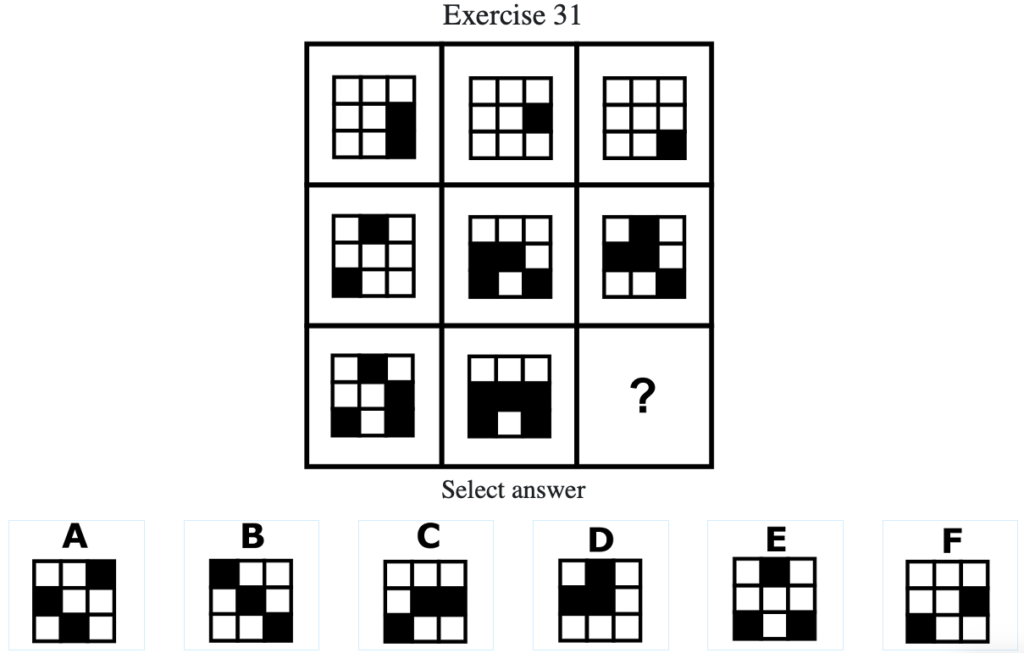
答え:「D」
解説:上中段から、左列の図形と中央列の図形を重ね合わせて、重複した部分が打ち消されることで右の列の図形になる。したがって答えは「D」となる(列方向にグルーピングしたときも同様に上の行の図形と中央の行の図形を重ね合わせて、重複した部分が打ち消されることで下の行の図形になる)。
Exercise 32
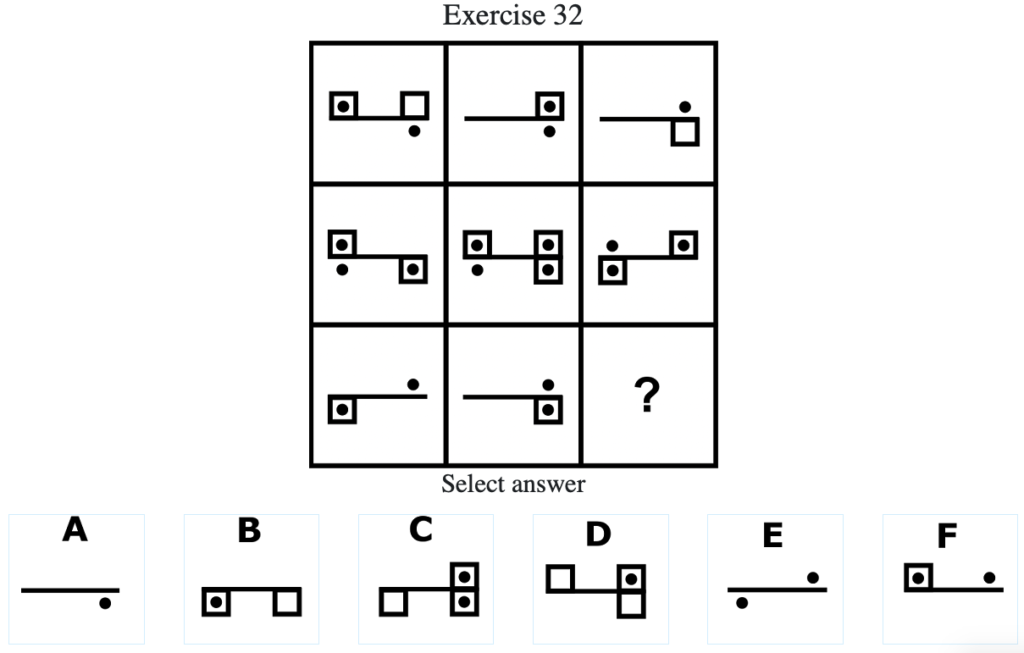
答え:「A」
解説:上中段より、左列と中央列の図形を重ね合わせて、重複しない部分を消して棒線を軸として反転すると右列の図形になる法則がわかる。したがって答えは「A」となる。
Exercise 33以降は格段に難易度が上がるため、図を用いて解説する。解説よりも図に注目していただきたい。
Exercise 33
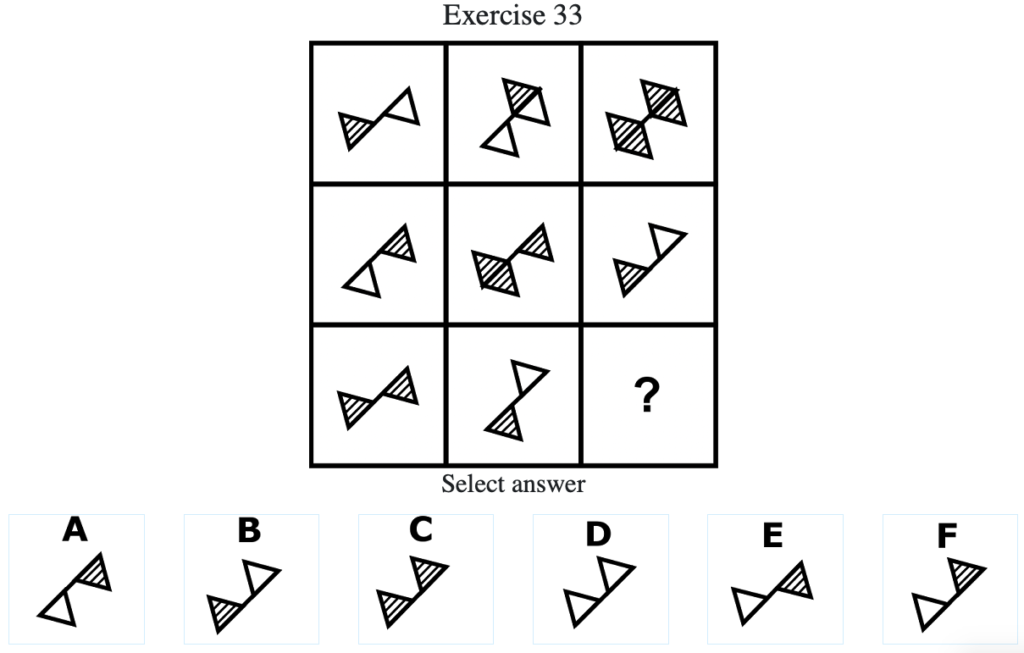
答え:「E」
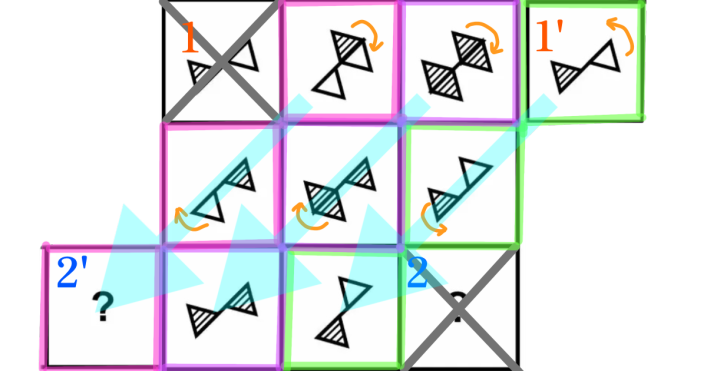
解説:おそらくノルウェーメンサのIQテストの問題の中で最難関の問題。図で同じ色の線で囲まれているマスのように右上から左下方向に斜めにグルーピングする(理解しやすいように1のマスを1’へ、2のマスを2’に移動する)。変化の始まりのマス(青い矢印の開始地点のマス)内の右側の三角形が2つ存在する場合は上の三角形が下に折り畳まれ(「斜線」と「白」の三角形が重なった場合は「斜線」の三角形となる)、1つだけの場合は反対方向に折り畳まれる。
斜めのグルーピングの中央のマスでは最初に折り畳まれた三角形と逆の位置にある左側の三角形が1度目の変化とは反対の方向に折り畳まれる。したがって答えに当てはまるのはピンクの線でグルーピングしたマスの白い三角形が上側に折り畳まれた「E」である。
Exercise 34
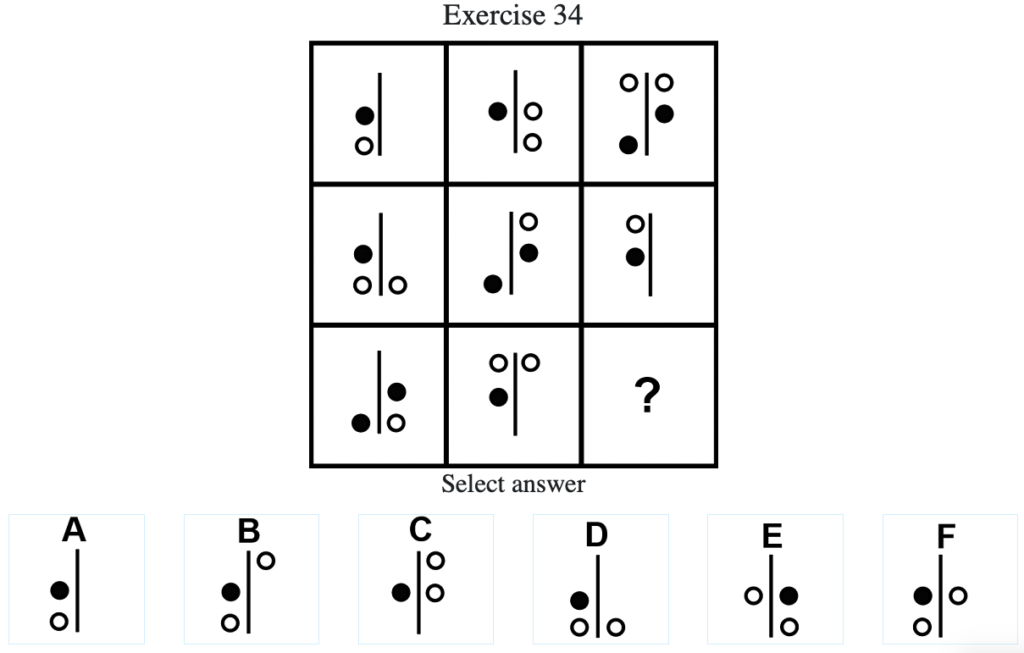
答え:「A」
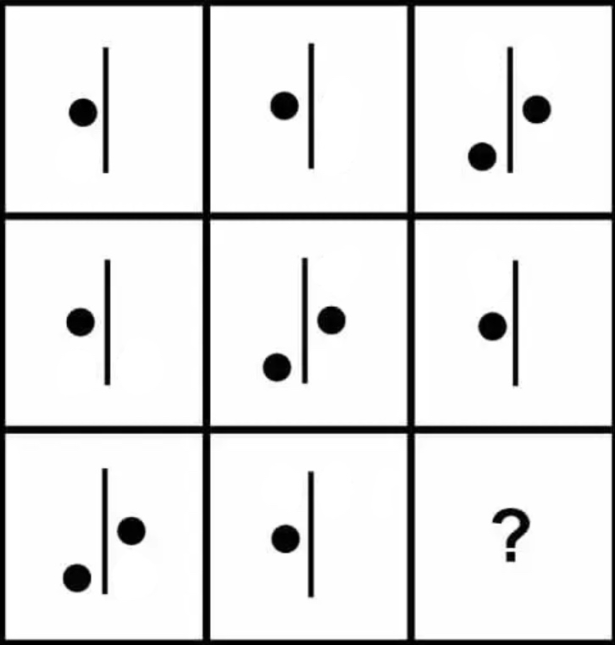
解説:白丸を消した図を上に示す。白丸を消すと黒丸の配置パターンが縦棒の左中央に1つだけの配置パターンAと縦棒の右中央と左下の2箇所にある配置パターンBがあることがわかる。黒丸の配置パターンは「A」→「A」→「B」→「A」→…の順番で変化し、黒丸と白丸が重なったときは白丸は黒丸の下に隠れる。行方向でグルーピングしたとき2個の白丸は縦棒の周りを反時計回りにそれぞれ2つずつ動くため答えは「A」となる(列方向でグルーピングして考えた場合、2個の白丸は反時計回りにそれぞれ1つずつ動く)。
Exercise 35
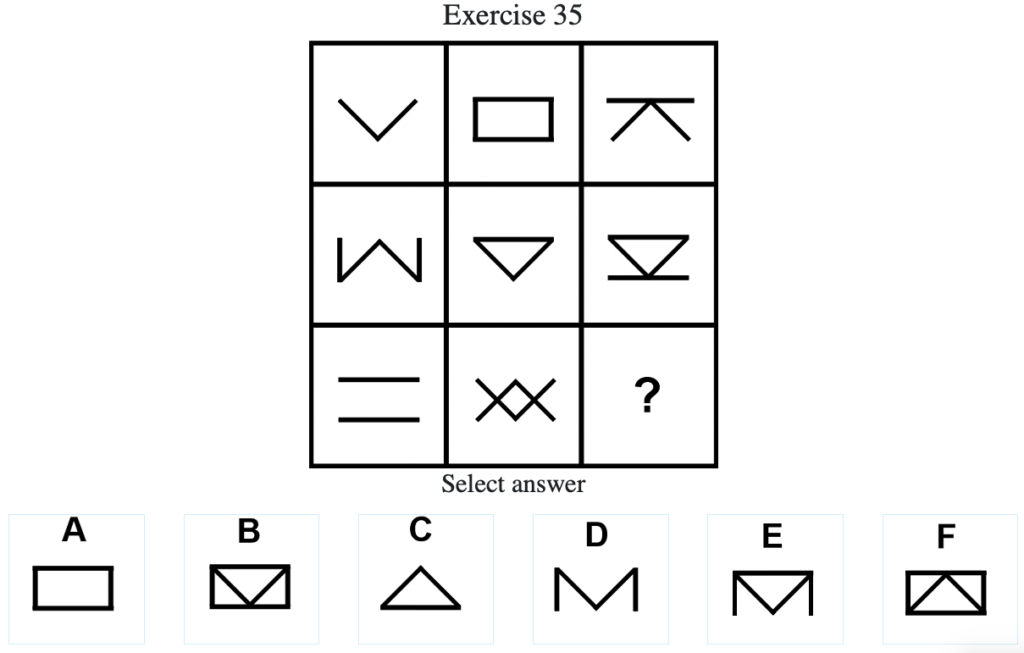
答え:「D」
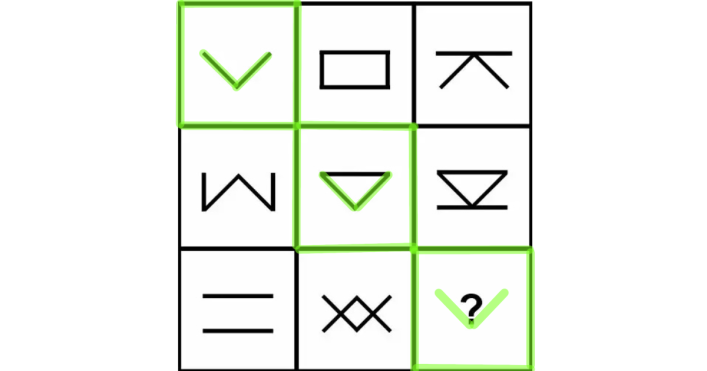
解説:上の図では左上から右下へ斜め方向に緑の線でグルーピングしている。緑の線で囲まれたグループでは「V」の形が共通しているため答えにも「V」の形が含まれると予想される…①
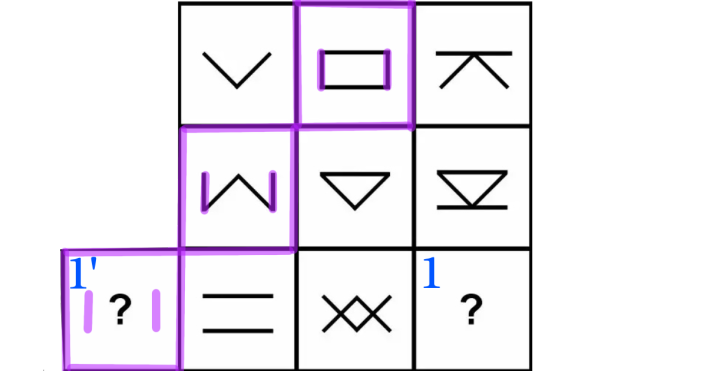
次に下の図では上段中央から左下方向に紫の線でグルーピングしている(理解しやすいように答えのマス1を1’に移動している)。紫の線で囲まれたグループでは「| |」の形が共通しているため答えにも「| |」の形が含まれると予想される…②
①と②より答えは「V」と「| |」の形で構成された図形であると予想されるので、答えは「D」となる。
解説は以上となります。お疲れ様でした!
あくまで個人的な意見ですが、初見でIQ135以上くらいのスコアが出た方ならおそらくJAPAN MENSAの入会テストも十分突破できると思います。
万一解説に不備があった場合はお問い合わせフォームまで連絡お願いします。



コメント
コメント一覧 (15件)
先ほど、テスト実施しました。
自己最高の128ポイントでした。
考え方はどうなのか?と検索したら
こちらに来ました。
回答、解説ありがとうございます。
コメント&当サイトをご覧いただきましてありがとうございます。
128ポイントも決して低い数字ではないのですごいと思います!
35の答えCじゃないですか?縦に足すとCだけ図形が違う気が、四角の中にxxみたいな?
コメントありがとうございます。めんどうなblog管理人の面堂です。
35の問題ですね。「縦に足す」というのは列(縦)方向に図形を重ね合わせるという意味ですか?
縦方向には法則性はないので、単純な列方向でのグルーピングはできないと思います。
また「Cだけ図形が違う」とはどういう意味でしょうか?
自分は記事内の図で示したように斜め方向で2つのグルーピングをし、共通する箇所を重ね合わせた「D」が正当だと考えています。
わざわざこんな辺鄙なサイトまで来てコメントしてくださったのは自分としてはとても嬉しいことなので、もしもまだ疑問に思っているのであれば、ちんたお様が納得して頂けるまで議論していきたいです。
ごめんなさい!パットみで書いちゃってwよく考えたらFじゃないですか?よこでもたてでも組み合わせると同じ図形できません?こういうのってどこかに答えないんですかねー 返信有ると思わなかったですびっくり。
なんかエラー出ちゃう、Fなら縦横を組み合わせた時に同じ形になりません? Cはなんか早とちりでミスりました!ごめんなさい、返信あってうれしいです
Fなら縦横を組み合わせた時に同じ形にはなりますが、行(横)方向で考えた時に上段と中段、列(縦)方向で考えた時に左列と中央列に法則性がありません(例:上段右は上段左と上段中央を重ね合わせた図形にはなっていない)。
これでは論理的矛盾が生じているため縦あるいは横方向でグルーピングすることができません。
IQテストでよくあるこのような行列推理の問題は基本的にグルーピングした向き(縦や横あるいは斜め)に法則性がないと成り立ちません。
Exercise35のような問題はぶっちゃけメンサの会員でも正しく解けない人は多いと思いますし、解釈は割れると思います。この問題だけ難易度が頭ひとつ抜けている印象です。
このような問題は単純に縦横でグルーピングすることができないので、そこからどう法則性を求め出すことができるかが問われるのです。
35ですが
右列と中列の模様を足し、足りない部分が左列になるかと思います。
?の箇所の模様は、上辺と下辺が無く、かつ、左右辺が在る模様ということで、Dになるかと思いました。
ご検証してみてください。
コメントありがとうございます。
ふむふむ、なるほど
論理的に破綻しているところがなさそうので、その考え方も正解だと思います!
例えば選択肢Dのアルファベットの「M」のような図形の他の選択肢にアルファベットの「W」のような形の図形があったら、はやりん様の考え方ではDとその「W」のような図形の2択を絞ることができなくなってしまいます。
しかしながら本問題にはそのような選択肢はないので、正当例のひとつだと思います⭕️
今度記事に追記しておきますね!
先ほど、IQ Test Made by Mensa Norway でテストをしてきました。
結果は、Exercise 33 を考えている途中で、時間切れとなり
IQ 132 と表示されました。
IQ テストはいつも解答がわからないまま終わっていましたが
こちらのおかげで初めて勉強できた気がします。
丁寧な解説で分かりやすかったです。
35は図形の左上と右上に時計の針のようなものがあると考え、それぞれ内側に向かって45度ずつ倒れていくのをイメージするとわかりやすいと思います。なので左下では無く、右下にグルーピングしてみてください。
34について
私は最初にこれを見たとき黒丸2つのパターンが右上のマスから左下のマスで共通しているように見えました。
そのため、右上から左下(斜め)にグルーピングして
1.黒丸固定
2.白丸が時計回りにひとつづつ移動
3.白丸が黒丸と重なったときは黒丸優先
という法則で A を選択しました。
Exercise18は別解がありますよ。
左2つの図形に十字(選択肢で言うとA)を足し込むと一番右の画像になります。
Exercise32について
□+□= ●となる説明が必要ですが、その説明がなかったように思われました。
私は、●=1, □=2 とし、3進法として考えてみました。
つまり、●+●=1+1=2=□、□+●=●+□=1+2= 0 (3進法)、□+□=2+2=1 (3進法)=●として考えました。
全部解きましたが、答えを確認するにはどうすればいいですか?